Generic Adhesive Contact Model
The Adhesive Rolling Resistance Linear Model is a new contact model now available in PFC 6 to represent a simple cohesive granular material. It is based on the two-dimensional model of Gilabert et al. (2007). The cohesion arises from a short-range attraction, which is a linear approximation of the van der Waals force law. The short-range attraction differs from the PFC bonded materials in that there is no concept of breakage (i.e., the attraction is always present whenever the interacting surfaces come within a specified attraction range). Gilabert et al. (2007) state that assemblies of cohesive grains exhibit much larger variations in their equilibrium densities than do corresponding assemblies of non-cohesive grains, because the cohesive grains may form loose, solid-like cohesive granulates. Such granular systems can stay in mechanical equilibrium at lower solid fractions (down to 25-30%) than cohesionless granular systems (with typical solid fractions of 58-64%). Cohesive granular materials have much less frequently been investigated by numerical simulation than cohesionless ones. The new contact model in PFC encompasses both types of materials and could be used to study macroscopic behavior of a variety of cohesive granular materials including cohesive powders such as xerographic toners (in which cohesion stems from van der Waals interaction) and wet bead packs (in which cohesion stems from liquid bridges joining neighboring particles).
This contact model provides the behavior of a cohesive granular material via a short-range attraction as a linear approximation of the van der Waals force by adding a cohesive component to the rolling resistance linear model. It is a linear-based model that can be installed at both ball-ball and ball-facet contacts. The cohesive component is characterized by two parameters: the maximum attractive force (F0), and the attraction range (D0), as in the following figure.
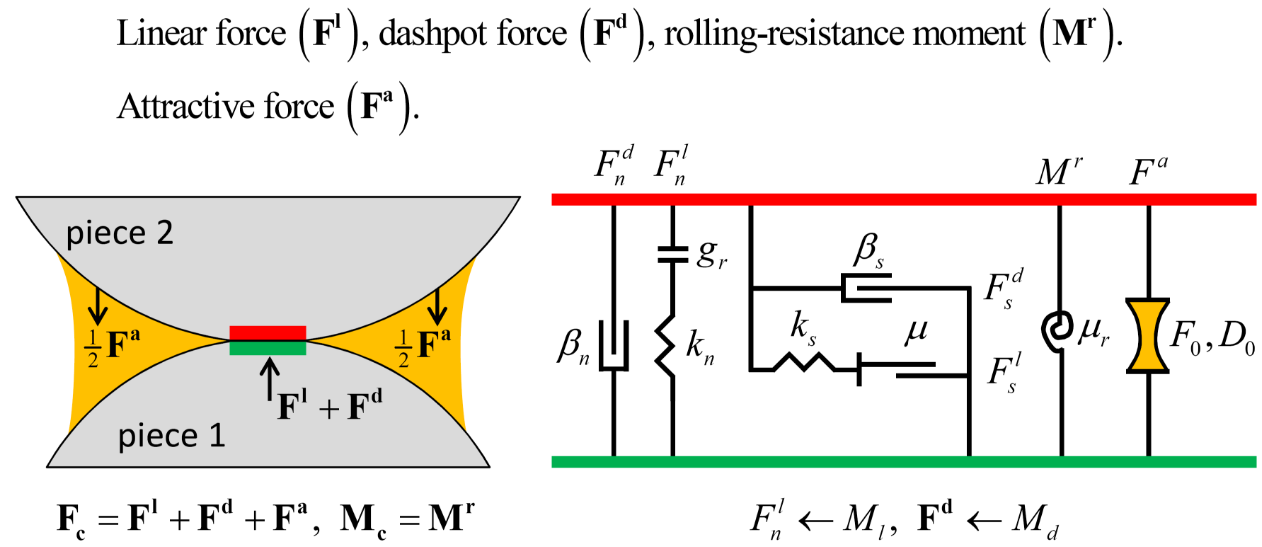
A contact with the adhesive rolling resistance linear model is active if and only if the surface gap is less than the attraction range, then the force-displacement law is skipped for inactive contacts. In addition to the energy partitions of the rolling resistance linear model, the adhesive rolling resistance linear model also partitions adhesive energy (i.e., work done by the attractive force on the contacting pieces). Refer to Gilabert et al. (2007) and Gilabert et al. (2008) for additional information about the structure and mechanical properties of cohesive granular materials as well as additional examples of cohesive packings studied in the laboratory.
Soft-Bond Contact Model
The soft-bond model can be used to simulate both unbonded and bonded systems.
In an unbonded state, it behaves essentially similar to the contact model proposed by Jiang (2015), providing the ability to transmit both a force and a moment at the contact point, with frictional strength parameters limiting the shear force, bending moment, and twisting moment.
In its bonded formulation, the behavior is similar to that of a linear parallel bond model, with a frictional strength parameter limiting the shear force, and the possibility for the bond to fail if the bond
strength is exceeded either in shear or in tension. However, contrary
to the linear parallel bond model, the bond is not removed upon failure.
Instead, it may enter into a softening
regime until the bond stress reaches a threshold value at which the
bond is removed and considered broken. The slope and tensile breakage
strength during softening can be
specified by the user (via the softening factor and the softening
tensile strength factor, respectively). Another difference with the
linear parallel bond model is that only one set of stiffnesses is used
for both the unbonded and bonded formulations. This behavior is
essentially similar to that proposed by Ma (2018),
with the difference that the bond elongation used to update the normal
stress in the softening regime accounts for both the normal displacement
and bending increments.
Behavior Summary
A soft bond can be envisioned as a set of elastic springs with
constant normal and shear stiffnesses, uniformly distributed over a
{rectangular in 2D; circular in 3D} cross-section lying on the contact
plane and centered at the contact point. Relative motion at the contact
causes a linear force and moment to develop, that act on the two
contacting pieces. If the bond is inactive, frictional strength
parameters cap the shear force, bending and twisting moments. If the
bond is active, the force and moment can be related to maximum normal
and shear stresses acting within the bond material at the bond
periphery. If either of these maximum stresses exceeds its corresponding
bond strength, the bond may enter a softening regime to a specified
failure criteria. After failure, the behavior reverts to the unbonded
formulation.
